Notes
Variations on Nested Designs
A short description of the post.

Split-Plot Designs
A short description of the post.
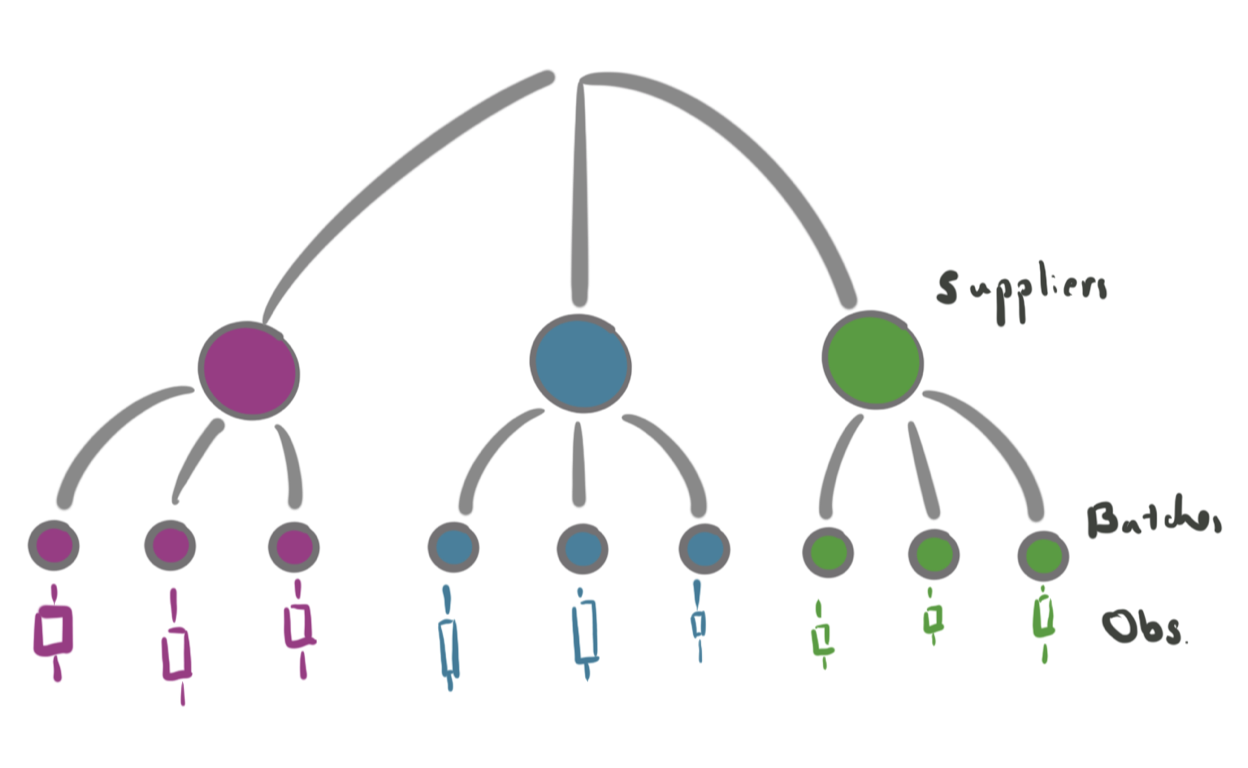
Nested Designs
A short description of the post.
Optimal Response Surface Designs
A short description of the post.

Mixture Experiments
A short description of the post.
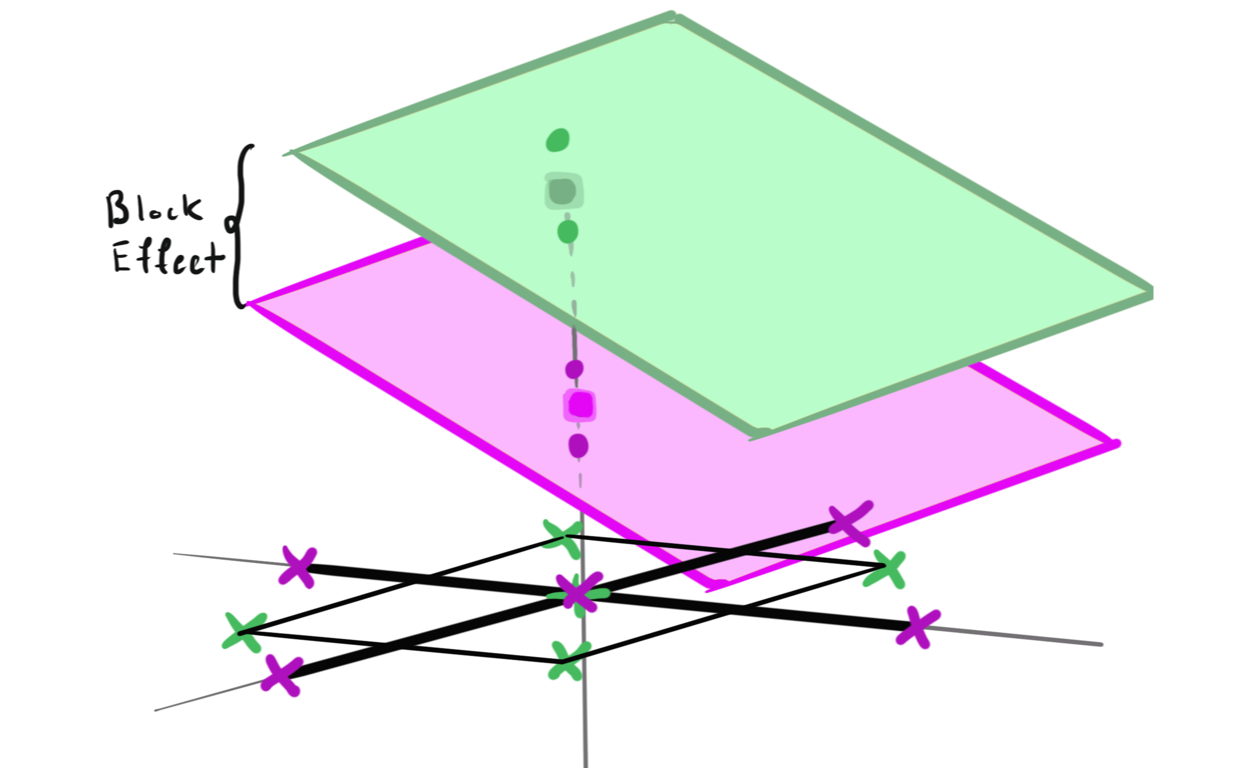
Blocking in Response Surface Designs
A short description of the post.
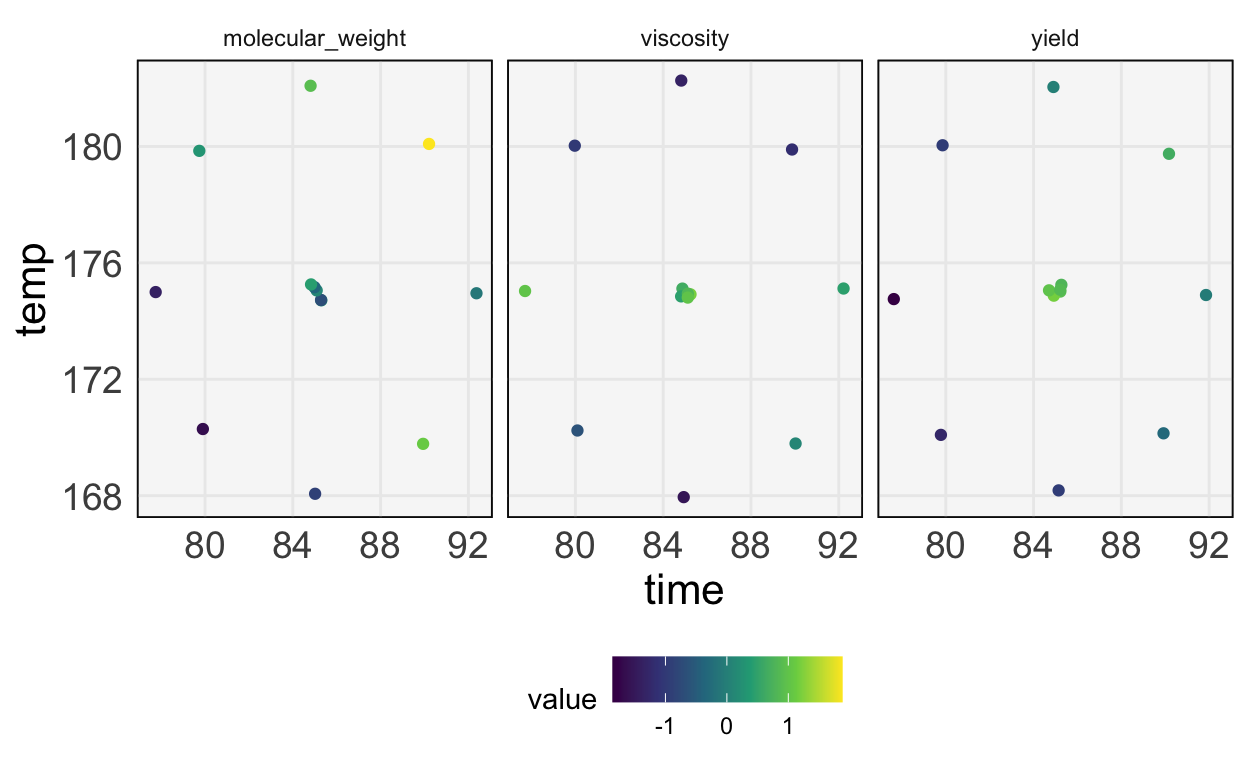
Optimizing Multiple Responses
Tracking several criteria simultaneously.
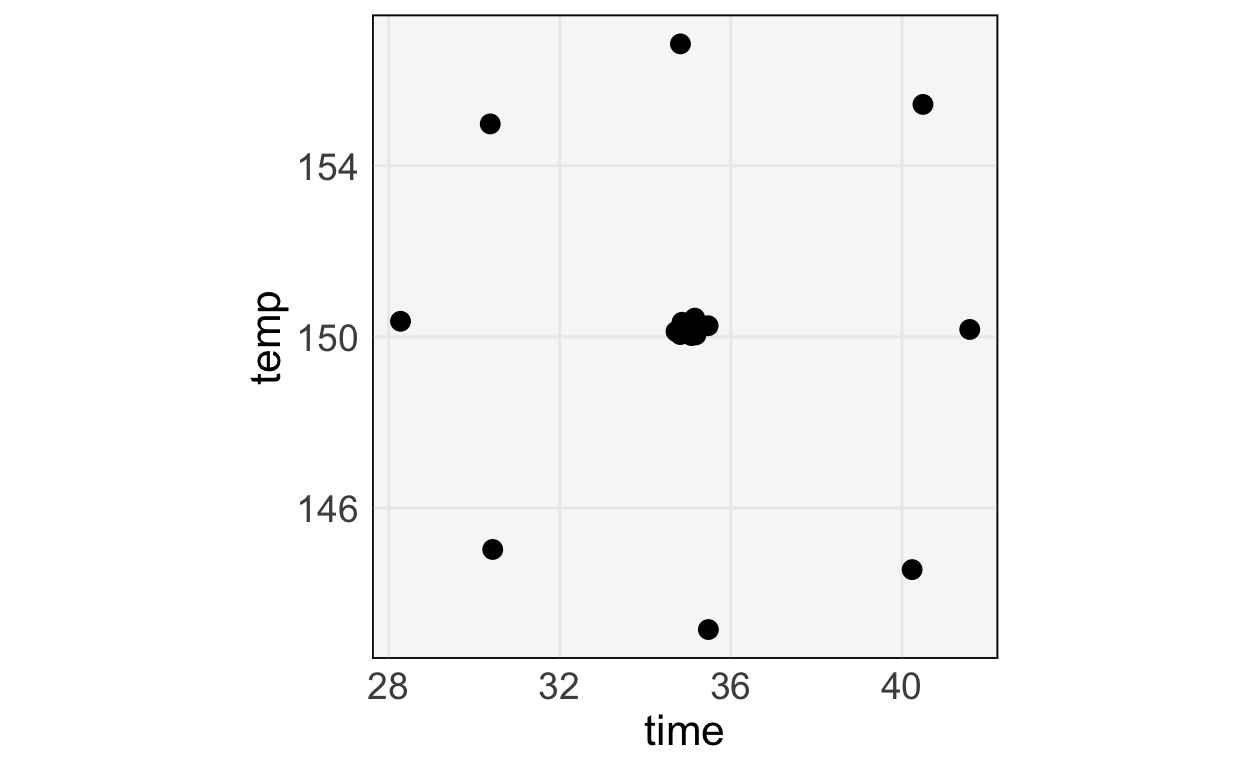
Designs for Response Surfaces
Where to sample along a response surface.
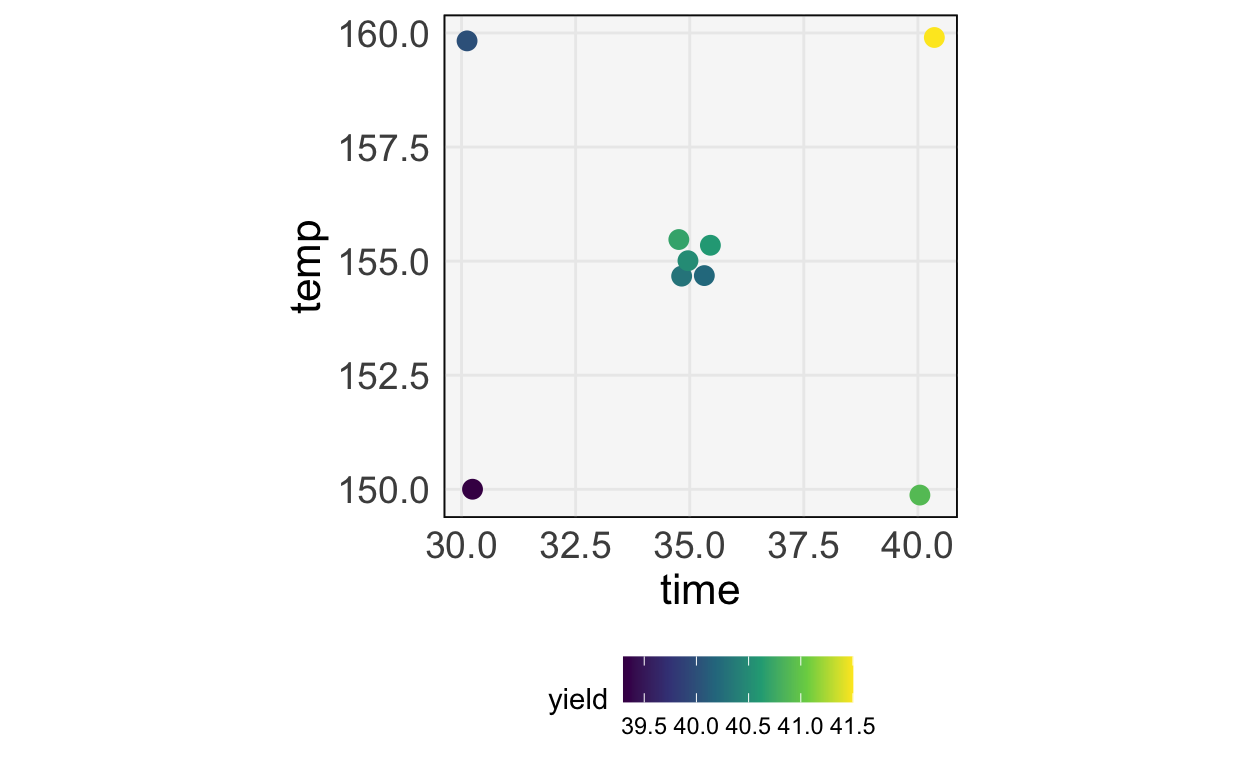
Method of Steepest Ascent
Sequential strategies for response surfaces.

Canonical Analysis
Characterizing optima in response surfaces.
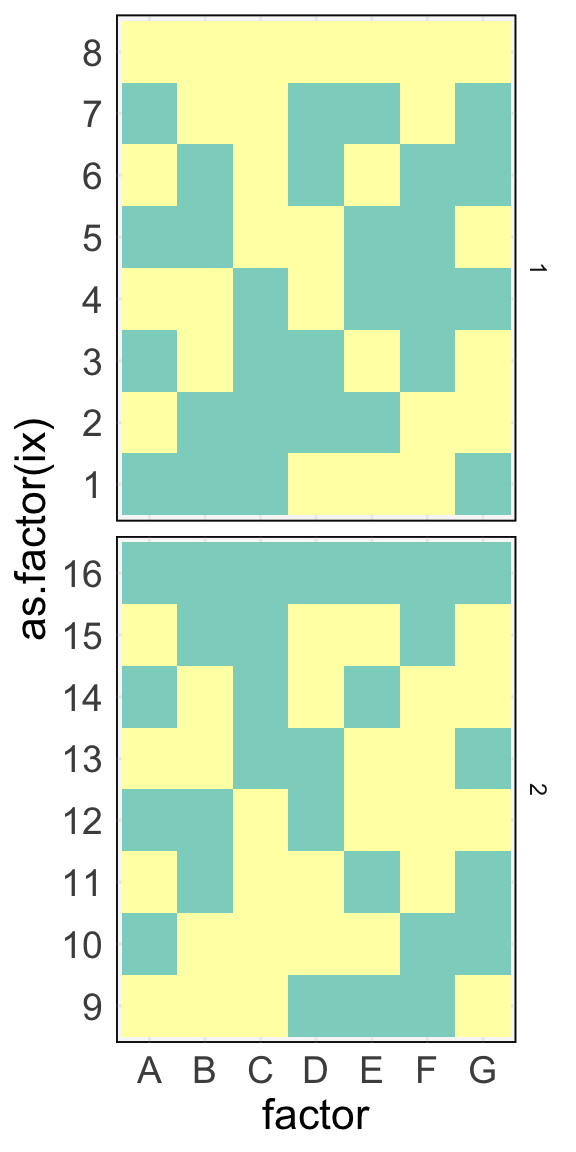
Foldover in $2^{K - p}$ Designs
Strategies for dealiasing effects in follow-up experiments.
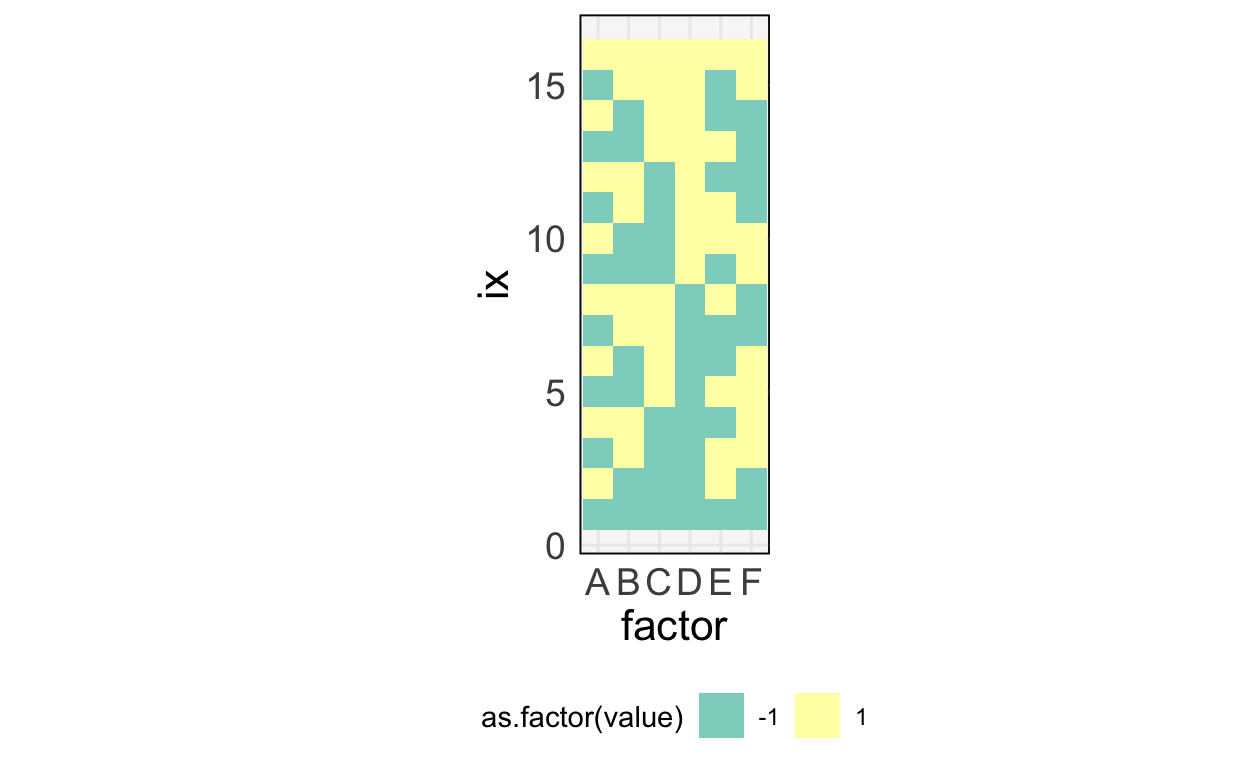
$2^{K - p}$ Fractional Factorial Designs
Even smaller fractions for more sample efficient experiments.
Projection and Blocking in $2^{K - p}$ Designs
Special considerations designing fractional factorials.
Saturated Designs
Very efficient analysis of a large set of factors.

Addition of Center Points
Extra points that help for checking nonlinearities.

$2^{K - 1}$ Fractional Factorial Designs
Reducing the number of samples required in factorial designs.

$2^K$ Designs and Regression
How effect estimates can be found using linear regression.

$2^K$ Designs are Optimal
Some notions of optimality in experimental design.

Examples of $2^K$ Designs
Three case studies in using $2^K$ designs.

Unreplicated $2^K$ Designs
Characterizing effects when only one replicate is available.
$2 ^ 3$ Factorial Design
A short description of the post.
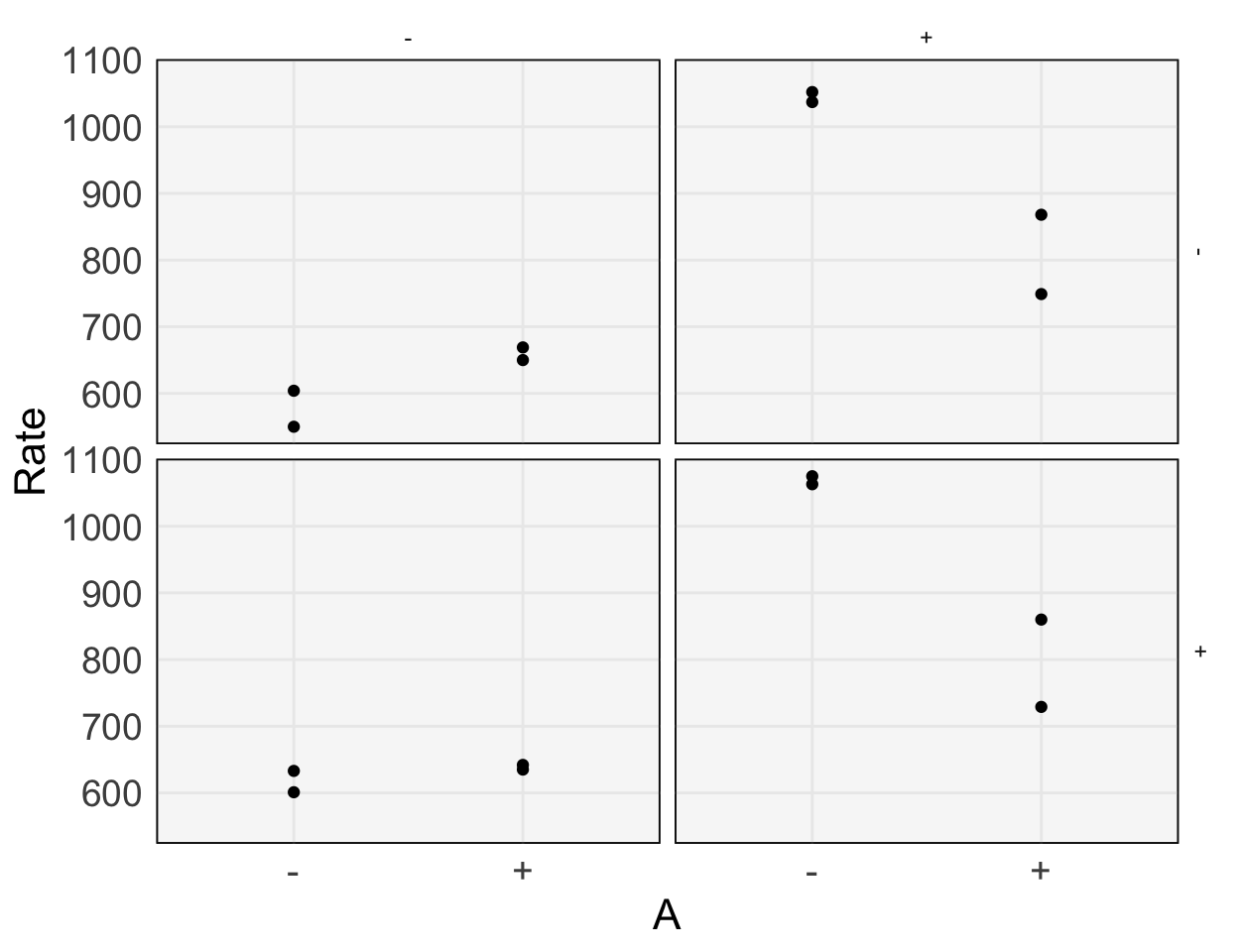
Interpreting effects in $2 ^ 3$ Designs
Testing, uncertainty, and visualization in $2^3$ designs.
$2^2$ Factorial Designs
Two factors each with two levels.

Interpreting Effects in $2^2$ Designs
Drawing conclusions from parameter estimates.
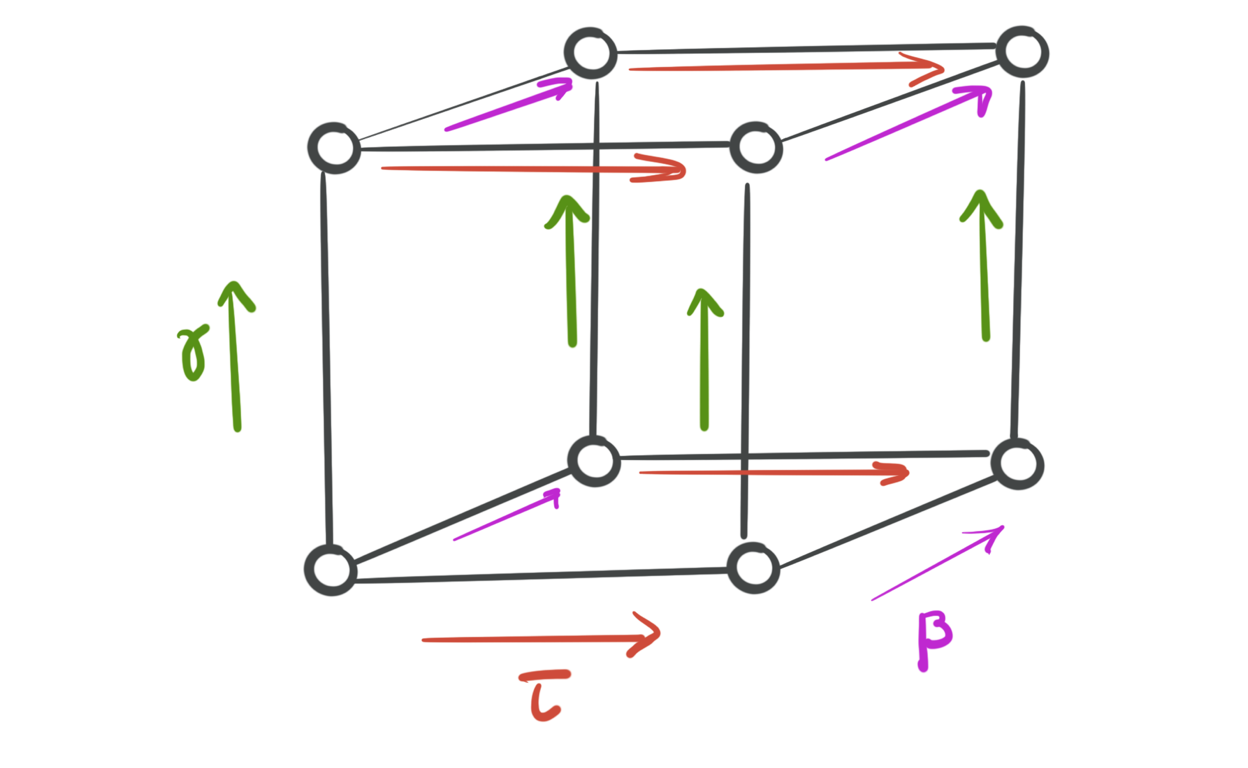
General Factorial Designs
Factorial designs with arbitrary numbers of factors
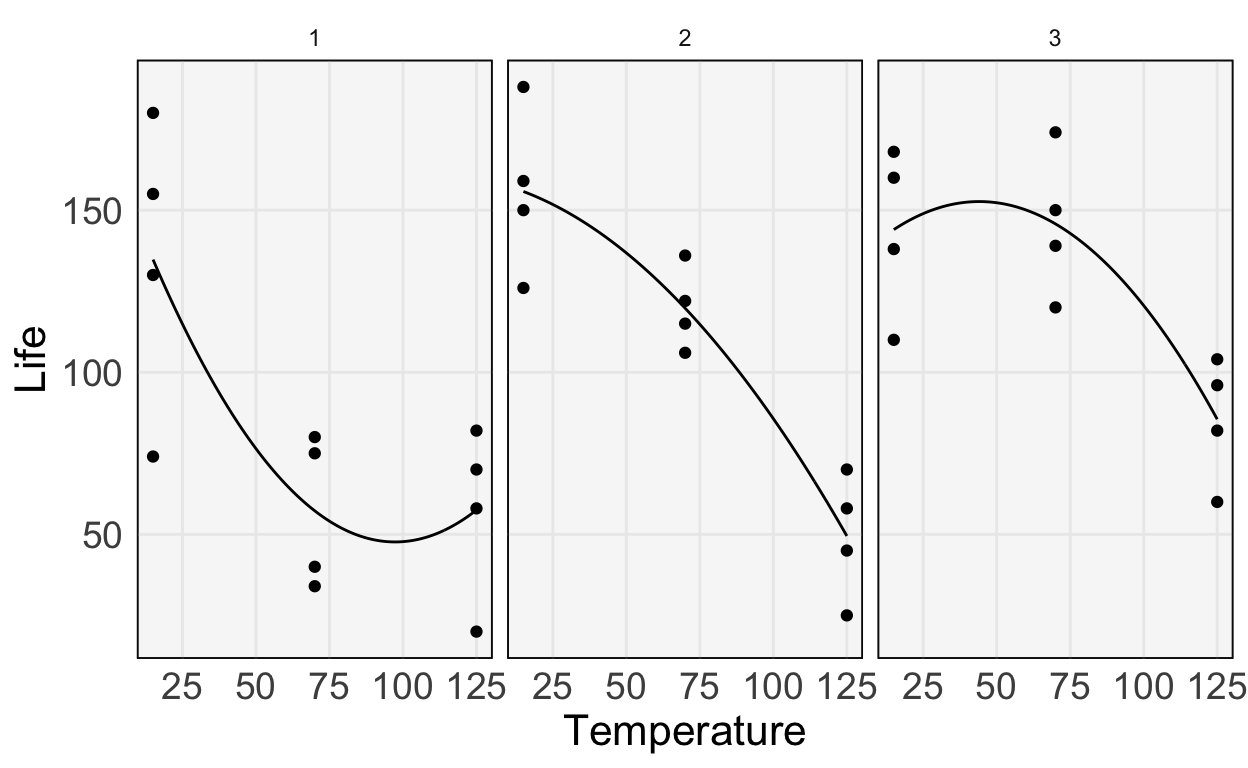
An Introduction to Response Surfaces
Flexibly modeling the relationship between factors and a response.
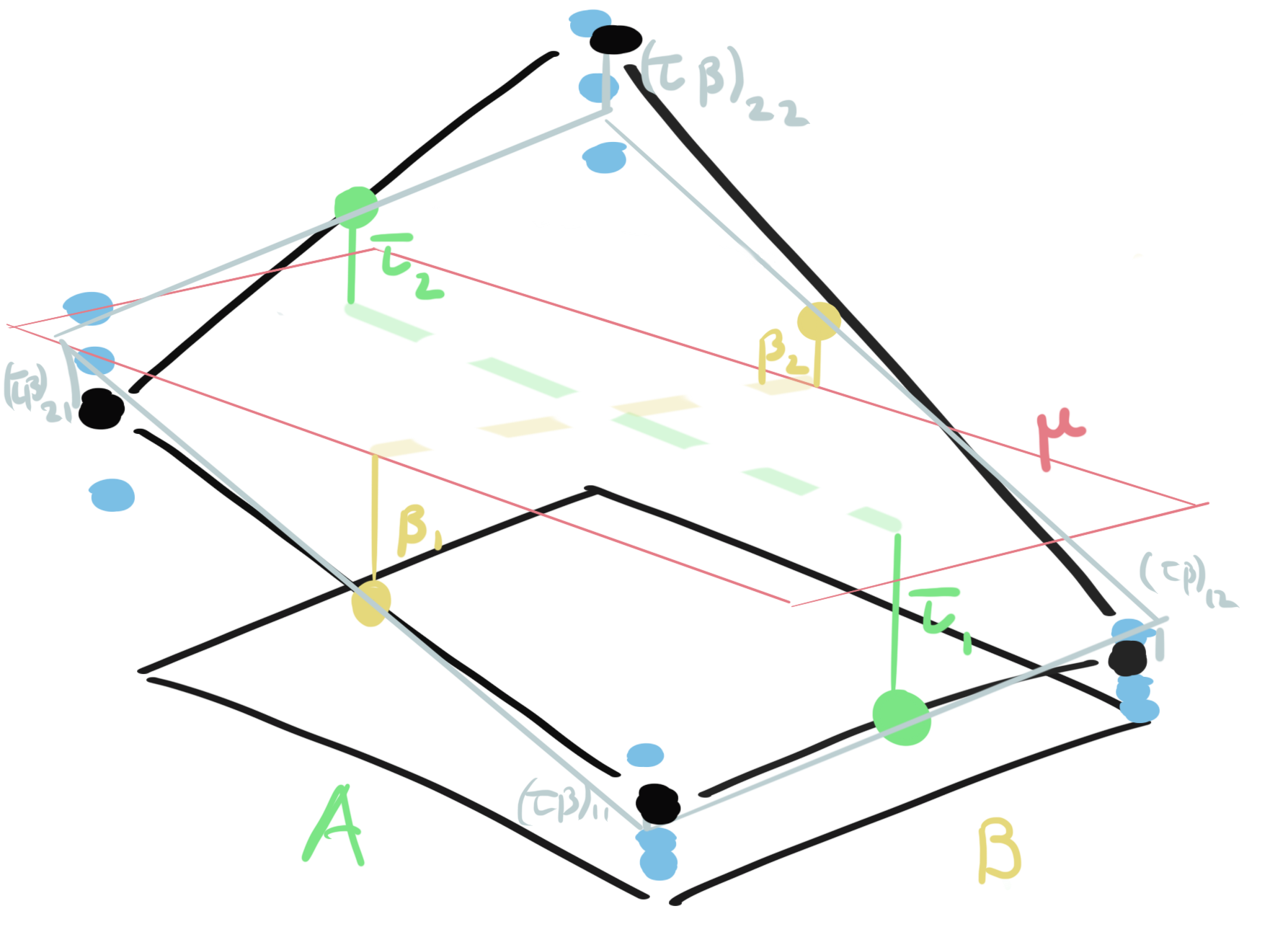
Two-Factor Factorial Design
Modeling and testing with two factors of interest

Following-up Two-Factor Fits
Multiple comparisons, model checking, and other post-estimation checks.
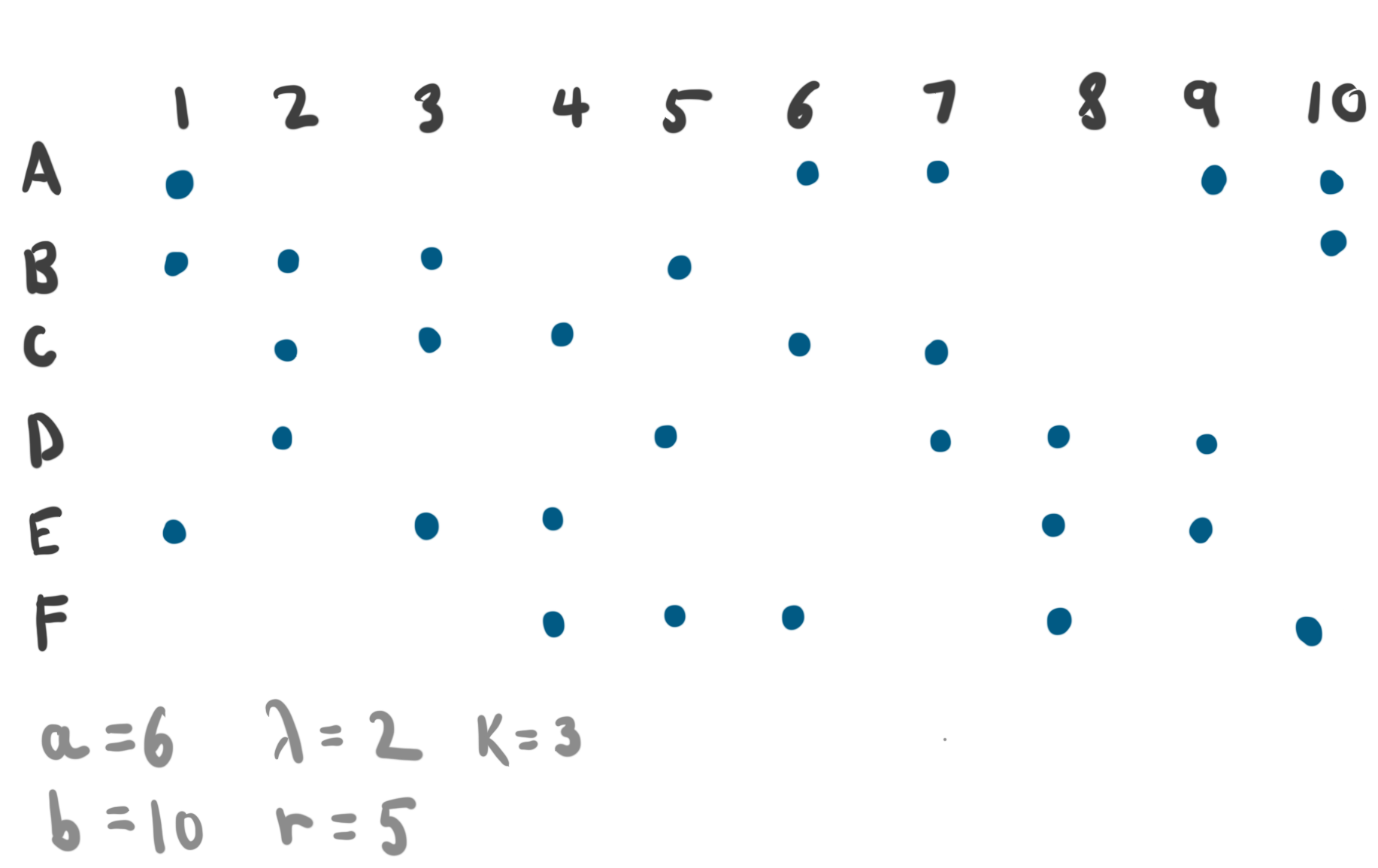
Balanced Incomplete Block Designs
An alternative to RCBDs in the limited sample setting
Introduction to Factorial Designs
Characterizing multiple facotrs in a single experiment.
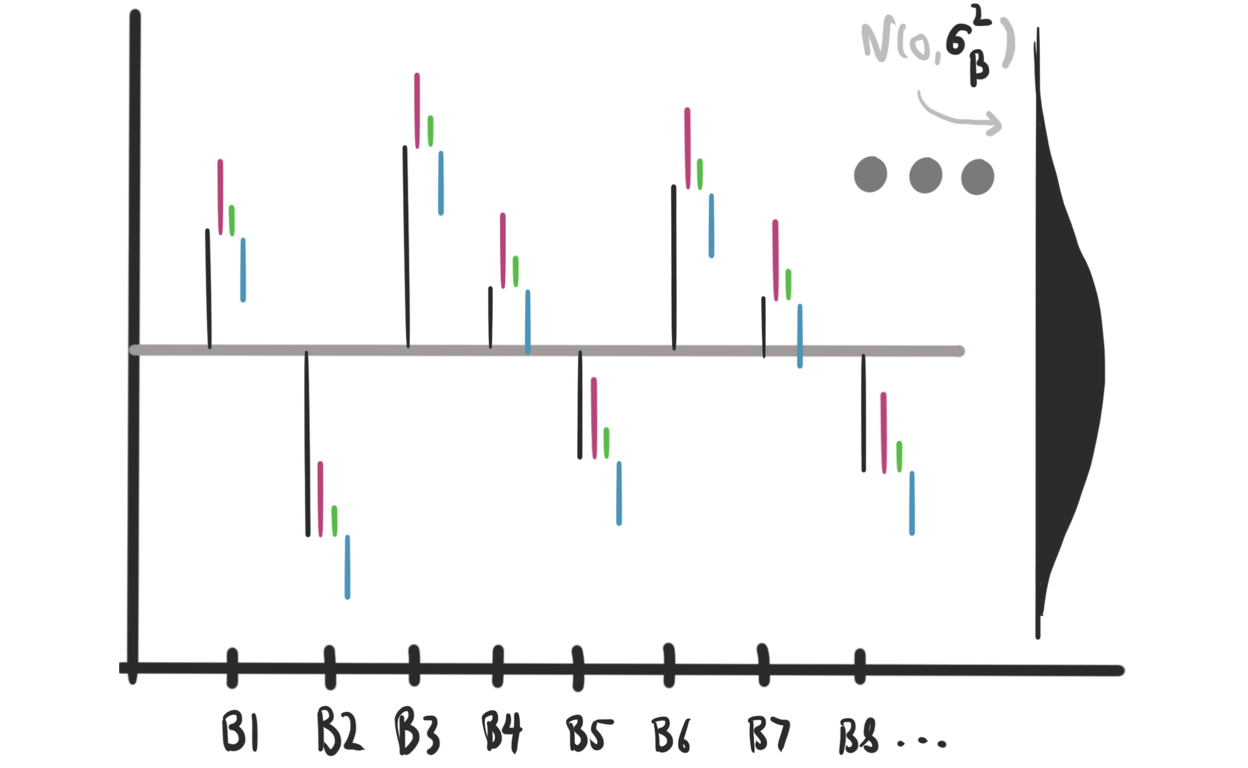
RCBD with Random Block Effects
The random effects analog of RCBD designs
Latin Squares, part 1
An alternative to RCBDs that works with two nuisance factors.
Latin Squares, part 2
Extensions of Latin Squares.
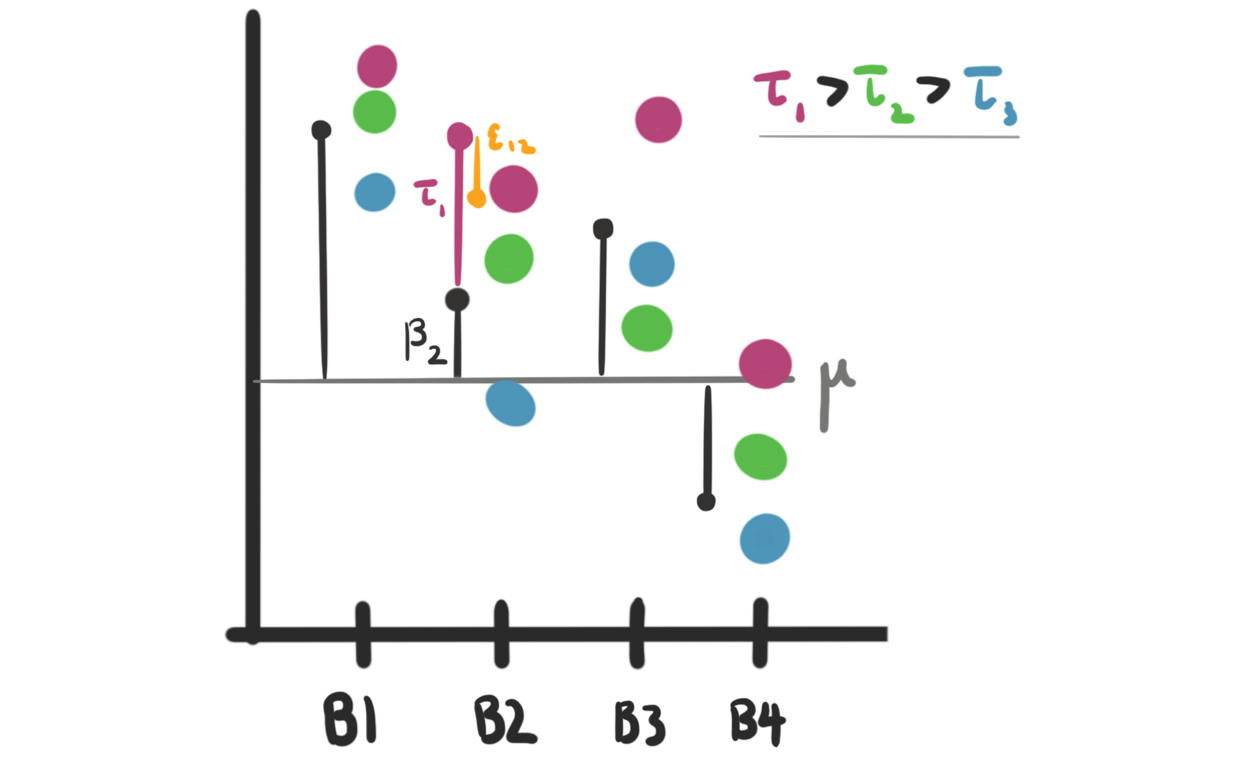
Randomized Complete Block Design
Dealing with batch effects using a generalization of pairing.

RCBD Diagnostics
Multiple comparison and model checks for RCBDs
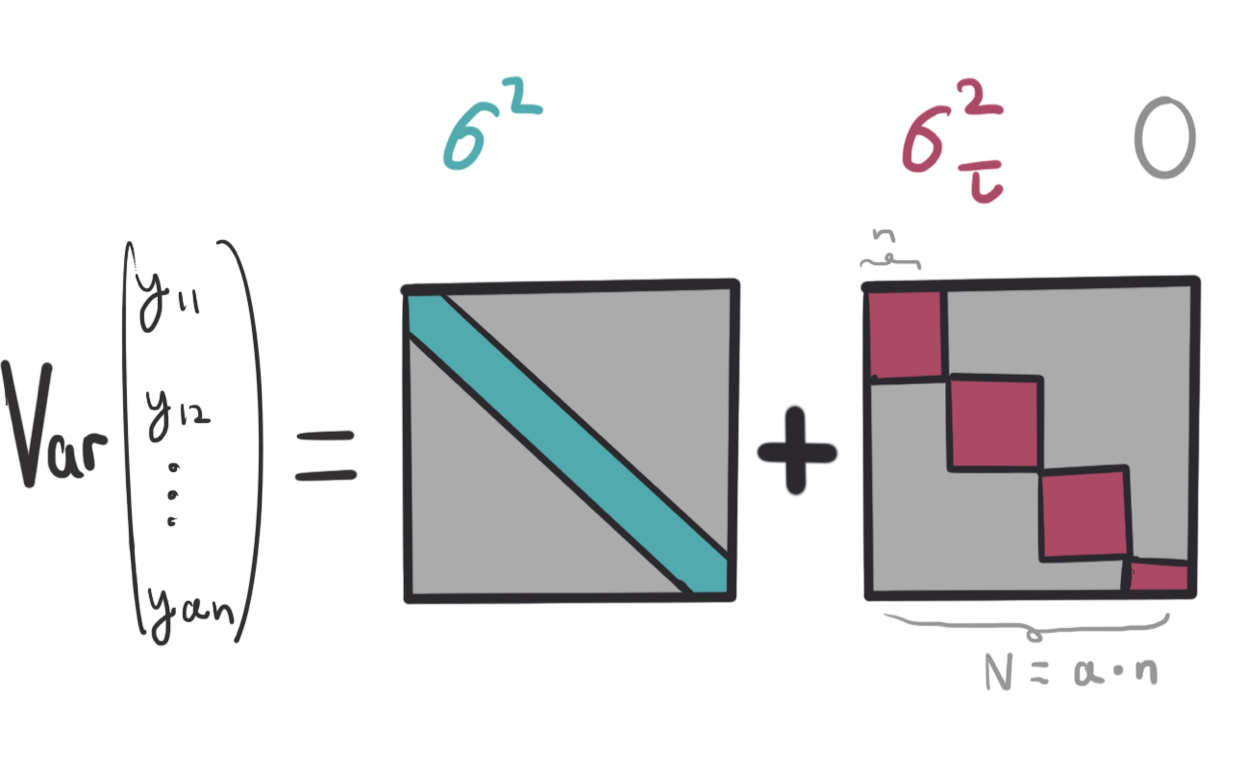
Fitting Random Effects
Using the method of moments or maximum likelihood to estimate parameters

Nonparametric ANOVA
A model-free alternative to ANOVA.
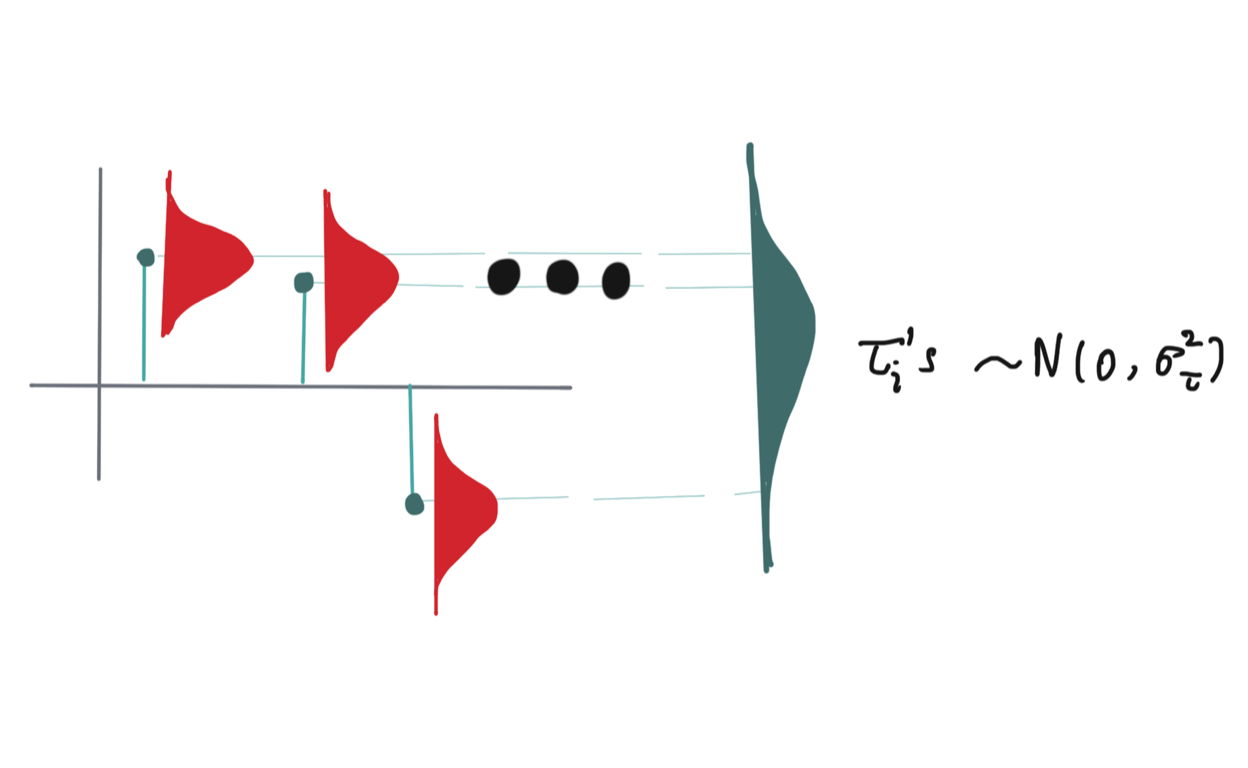
Random Effects
An introduction to random effects models
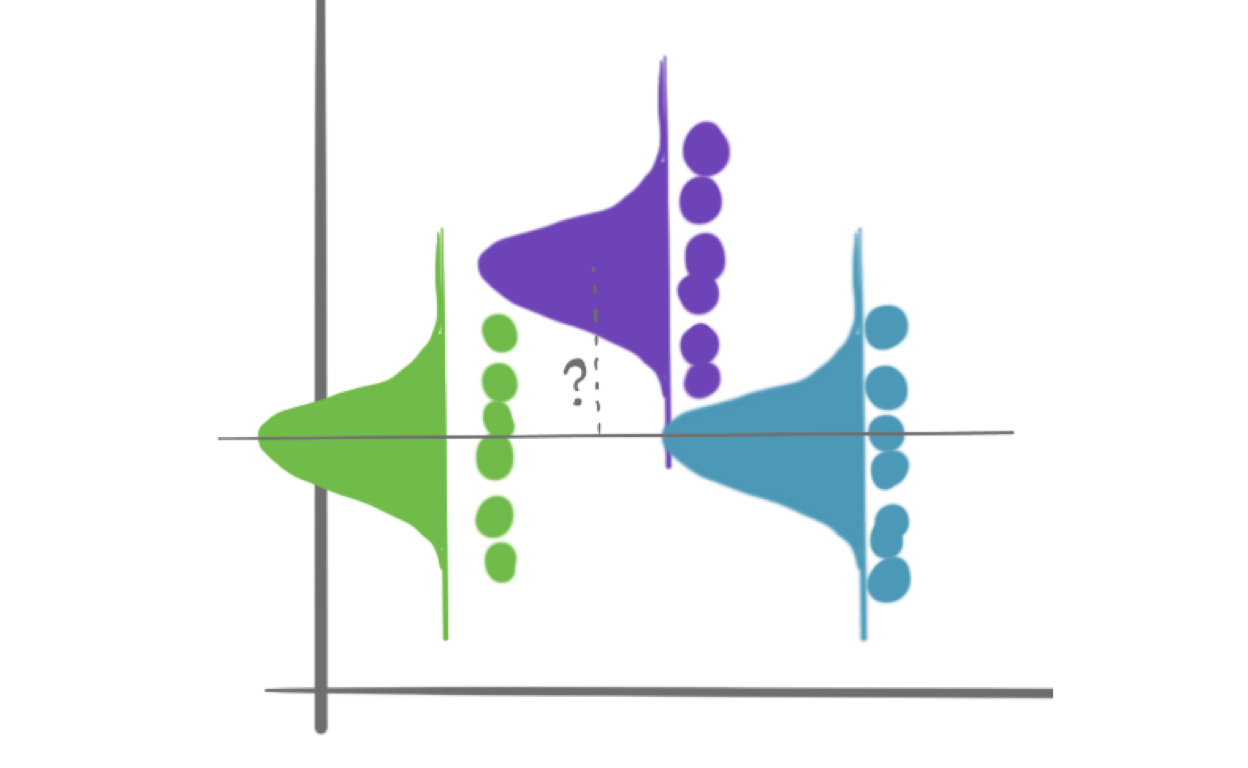
Contrasts
Making pointed comparisons between treatment levels in ANOVA

Multiple Comparisons
The multiple comparisons problem and some solutions.

ANOVA
The ANOVA model and sum-of-squares decomposition
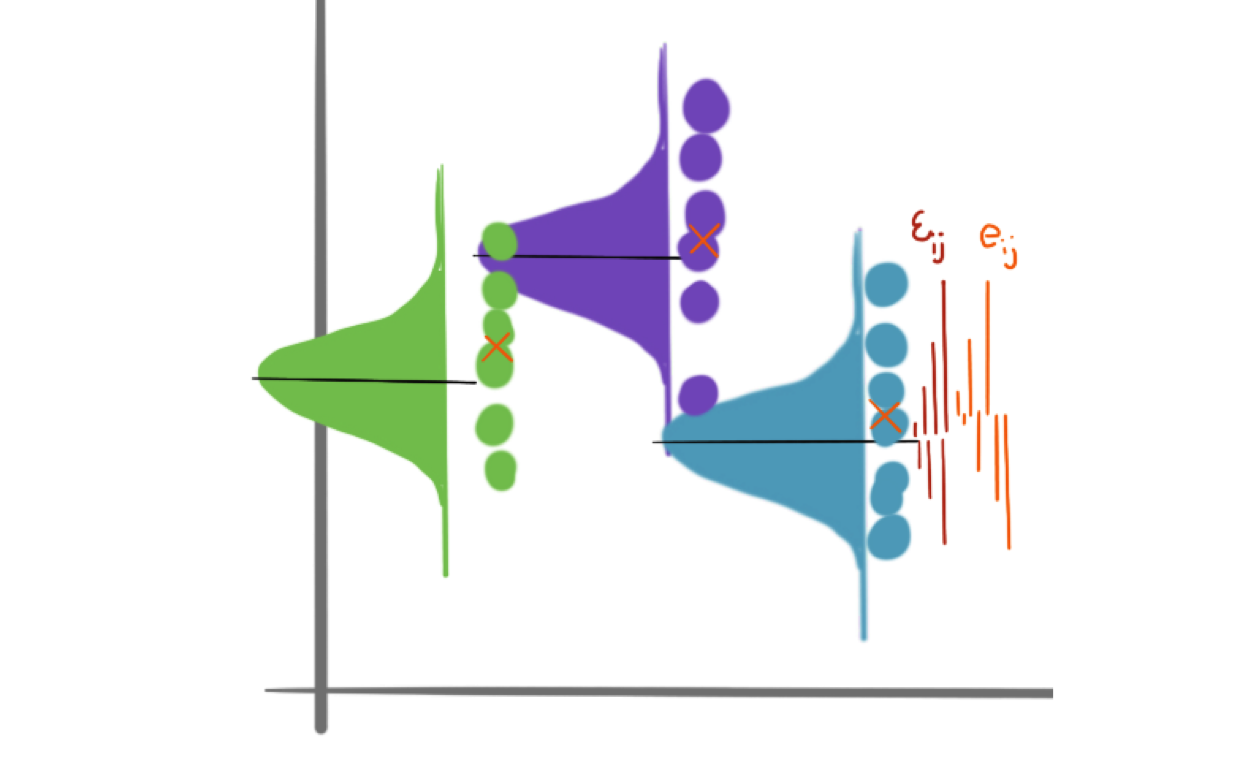
Model Checking
How should we check the assumptions of the ANOVA model?
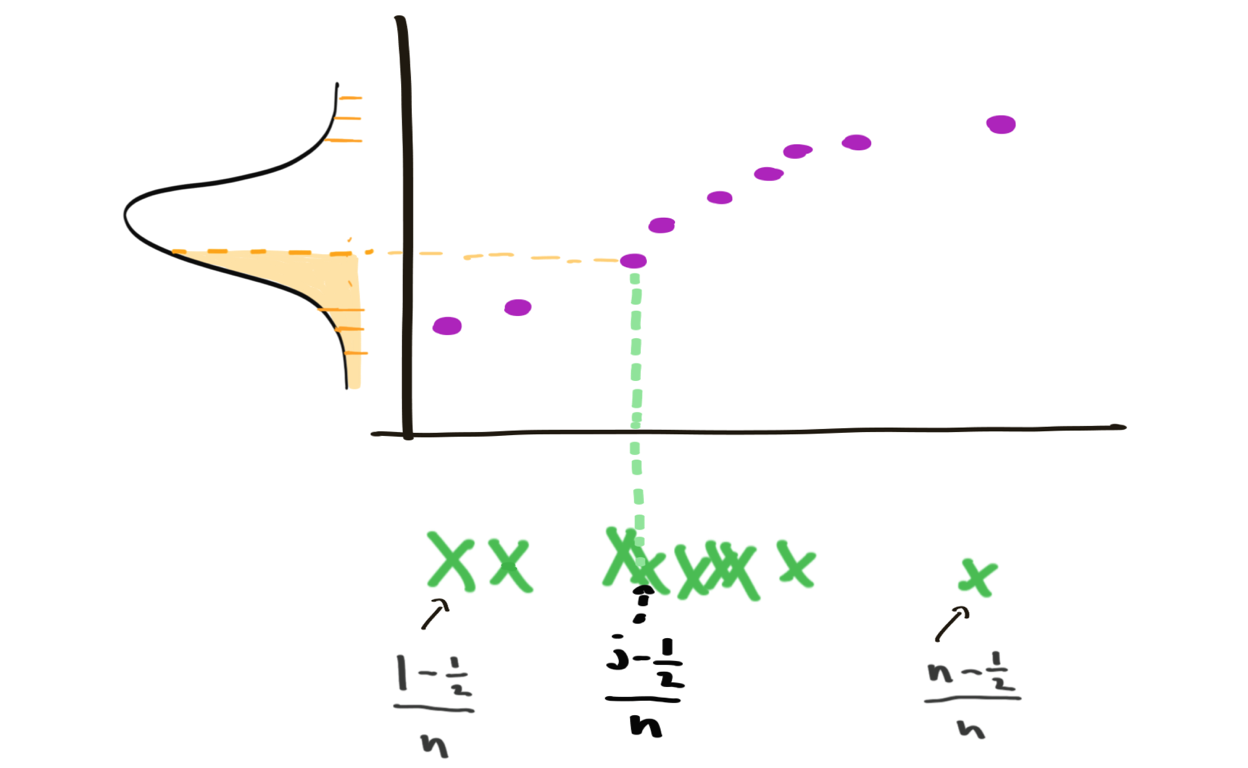
Diagnostics and Power
Tricks to make sure tests aren't applied blindly
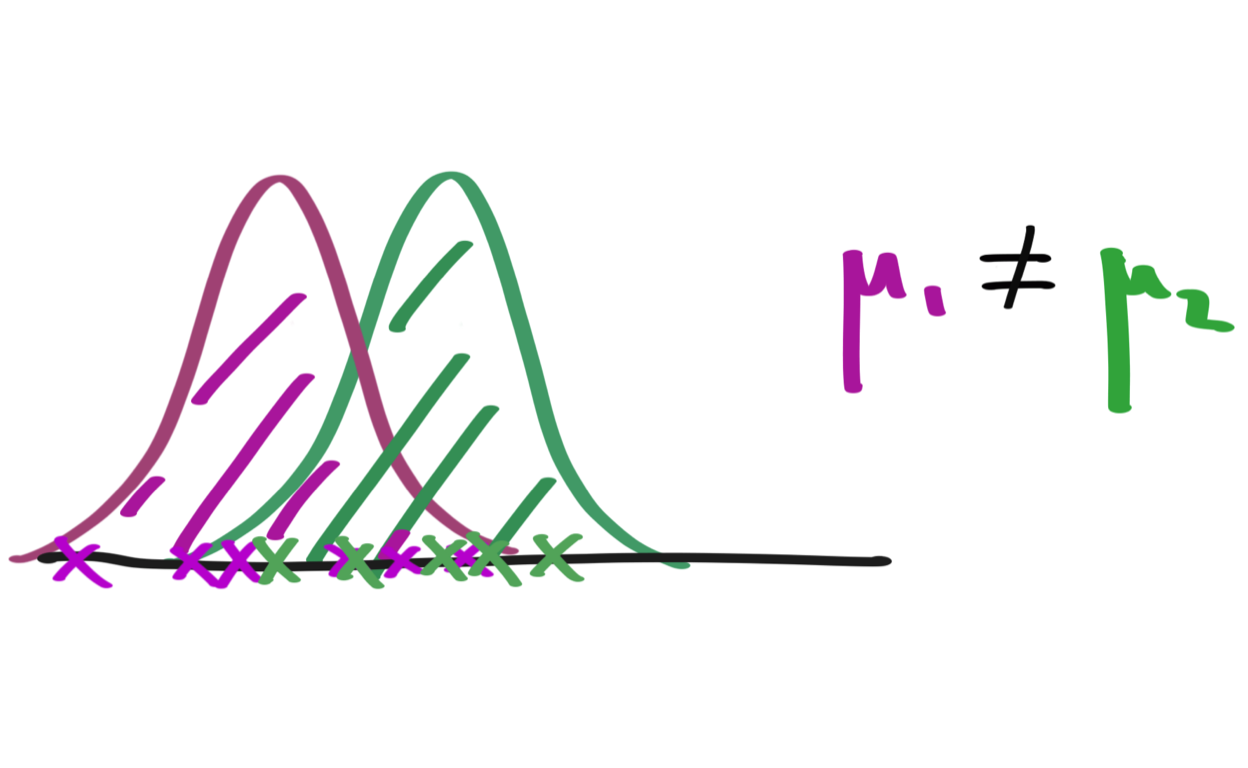
Testing Differences in Means
The basic principles of hypothesis testing.
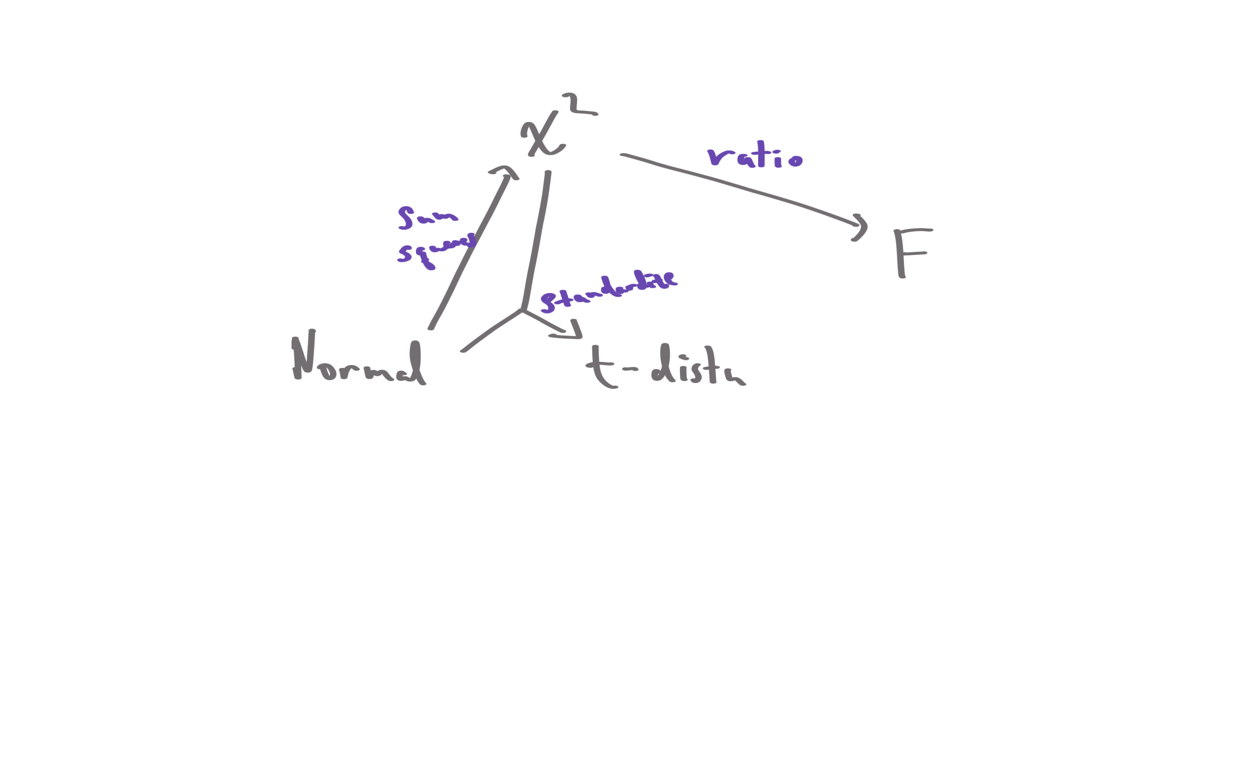
Common Distributions
Distributions that appear across experimental design.
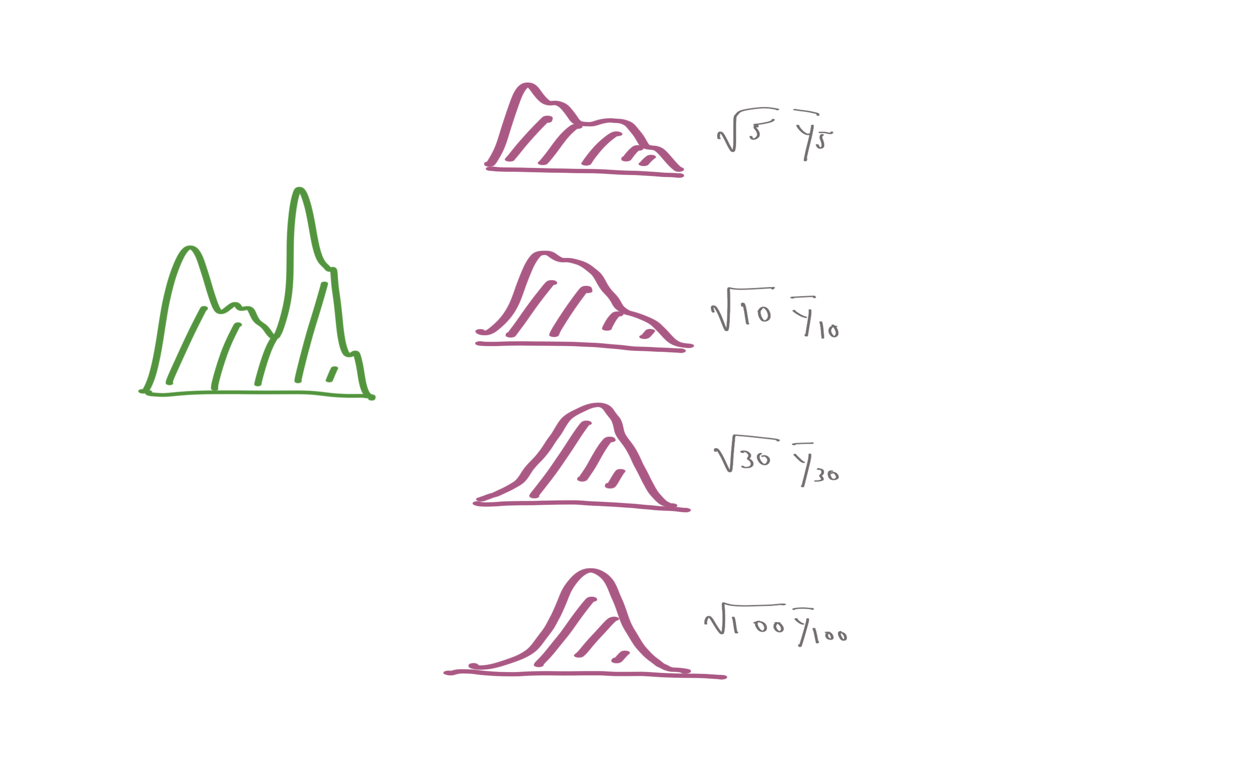
Probability Review
Probability distributions, their properties, and relationships.

Principles and Vocabulary
An introduction to randomization, replication, and blocking.
Motivating Examples
Why are experiments run in the first place?