Principal Components Analysis
Linear dimensionality reduction with PCA
library(tidyverse)
library(tidymodels)
-
For low-dimensional data, we could visually encode all the features in our data directly, either using properties of marks or through faceting. In high-dimensional data, this is no longer possible. However, though there are many features associated with each observation, it may still be possible to organize samples across a smaller number of meaningful, derived features. In the next week, we’ll explore a few ways of partially automating the search for relevant features.
-
An important special case for dimensionality reduction emerges when we make the following assumptions about the set of derived features,
- Features that are linear combinations of the raw input columns.
- Features that are orthogonal to one another.
- Features that have high variance.
-
Why would we want features to have these properties?
- Restricting to linear combinations allows for an analytical solution. We will relax this requirement when discussing UMAP.
- Orthogonality means that the derived features will be uncorrelated with one another. This is a nice property, because it would be wasteful if features were redundant.
- High variance is desirable because it means we preserve more of the essential structure of the underlying data. For example, if you look at this 2D representation of a 3D object, it’s hard to tell what it is,

What is this object?
-
But when viewing an alternative reduction which has higher variance…

Not so complicated now. Credit for this example goes to Professor Julie Josse, at Ecole Polytechnique.
-
Principal Components Analysis (PCA) is the optimal dimensionality reduction under these three restrictions, in the sense that it finds derived features with the highest variance. Formally, PCA finds a matrix Φ ∈ ℝD × K and a set of vectors zi ∈ ℝK such that xi = Φ**zi for all i. The columns of Φ are called principal components, and they specify the structure of the derived linear features. The vector zi is called the score of xi with respect to these components. The top component explains the most variance, the second captures the next most, and so on. Geometrically, the columns of Φ span a plane that approximates the data. The zi provide coordinates of points projected onto this plane.
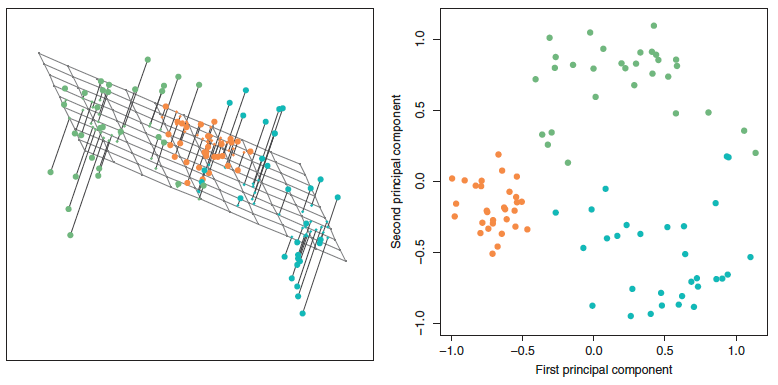
Figure 3: PCA finds a low-dimensional linear subspace that closely approximates the high-dimensional data.
-
In R, PCA can be conveniently implemented using the tidymodels package. The dataset below contains properties of a variety of cocktails, from the Boston Bartender’s guide. The first two columns are qualitative descriptors, while the rest give numerical ingredient information.
cocktails_df <- read_csv("https://uwmadison.box.com/shared/static/qyqof2512qsek8fpnkqqiw3p1jb77acf.csv") cocktails_df[, 1:6] ## # A tibble: 937 × 6 ## name category light_rum lemon_…¹ lime_…² sweet…³ ## <chr> <chr> <dbl> <dbl> <dbl> <dbl> ## 1 Gauguin Cocktail Classics 2 1 1 0 ## 2 Fort Lauderdale Cocktail Classics 1.5 0 0.25 0.5 ## 3 Cuban Cocktail No. 1 Cocktail Classics 2 0 0.5 0 ## 4 Cool Carlos Cocktail Classics 0 0 0 0 ## 5 John Collins Whiskies 0 1 0 0 ## 6 Cherry Rum Cocktail Classics 1.25 0 0 0 ## 7 Casa Blanca Cocktail Classics 2 0 1.5 0 ## 8 Caribbean Champagne Cocktail Classics 0.5 0 0 0 ## 9 Amber Amour Cordials and Liqueurs 0 0.25 0 0 ## 10 The Joe Lewis Whiskies 0 0.5 0 0 ## # … with 927 more rows, and abbreviated variable names ¹lemon_juice, ## # ²lime_juice, ³sweet_vermouth -
The
pca_recobject below defines a tidymodels recipe for performing PCA. Computation of the lower-dimensional representation is deferred untilprep()is called. This delineation between workflow definition and execution helps clarify the overall workflow, and it is typical of the tidymodels package.pca_rec <- recipe(~., data = cocktails_df) %>% update_role(name, category, new_role = "id") %>% step_normalize(all_predictors()) %>% step_pca(all_predictors()) pca_prep <- prep(pca_rec) -
We can tidy each element of the workflow object. Since PCA was the second step in the workflow, the PCA components can be obtained by calling tidy with the argument “2.” The scores of each sample with respect to these components can be extracted using
juice. The amount of variance explained by each dimension is also given by tidy, but with the argumenttype = "variance".tidy(pca_prep, 2) ## # A tibble: 1,600 × 4 ## terms value component id ## <chr> <dbl> <chr> <chr> ## 1 light_rum 0.163 PC1 pca_tMJA6 ## 2 lemon_juice -0.0140 PC1 pca_tMJA6 ## 3 lime_juice 0.224 PC1 pca_tMJA6 ## 4 sweet_vermouth -0.0661 PC1 pca_tMJA6 ## 5 orange_juice 0.0308 PC1 pca_tMJA6 ## 6 powdered_sugar -0.476 PC1 pca_tMJA6 ## 7 dark_rum 0.124 PC1 pca_tMJA6 ## 8 cranberry_juice 0.0954 PC1 pca_tMJA6 ## 9 pineapple_juice 0.119 PC1 pca_tMJA6 ## 10 bourbon_whiskey 0.0963 PC1 pca_tMJA6 ## # … with 1,590 more rows juice(pca_prep) ## # A tibble: 937 × 7 ## name category PC1 PC2 PC3 PC4 PC5 ## <fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 Gauguin Cocktail Classics 1.38 -1.15 1.34 -1.12 1.52 ## 2 Fort Lauderdale Cocktail Classics 0.684 0.548 0.0308 -0.370 1.41 ## 3 Cuban Cocktail No. 1 Cocktail Classics 0.285 -0.967 0.454 -0.931 2.02 ## 4 Cool Carlos Cocktail Classics 2.19 -0.935 -1.21 2.47 1.80 ## 5 John Collins Whiskies 1.28 -1.07 0.403 -1.09 -2.21 ## 6 Cherry Rum Cocktail Classics -0.757 -0.460 0.909 0.0154 -0.748 ## 7 Casa Blanca Cocktail Classics 1.53 -0.392 3.29 -3.39 3.87 ## 8 Caribbean Champagne Cocktail Classics 0.324 0.137 -0.134 -0.147 0.303 ## 9 Amber Amour Cordials and Liqu… 1.31 -0.234 -1.55 0.839 -1.19 ## 10 The Joe Lewis Whiskies 0.138 -0.0401 -0.0365 -0.100 -0.531 ## # … with 927 more rows tidy(pca_prep, 2, type = "variance") ## # A tibble: 160 × 4 ## terms value component id ## <chr> <dbl> <int> <chr> ## 1 variance 2.00 1 pca_tMJA6 ## 2 variance 1.71 2 pca_tMJA6 ## 3 variance 1.50 3 pca_tMJA6 ## 4 variance 1.48 4 pca_tMJA6 ## 5 variance 1.37 5 pca_tMJA6 ## 6 variance 1.32 6 pca_tMJA6 ## 7 variance 1.30 7 pca_tMJA6 ## 8 variance 1.20 8 pca_tMJA6 ## 9 variance 1.19 9 pca_tMJA6 ## 10 variance 1.18 10 pca_tMJA6 ## # … with 150 more rows -
We can interpret components by looking at the linear coefficients of the variables used to define them. From the plot below, we see that the first PC mostly captures variation related to whether the drink is made with powdered sugar or simple syrup. Drinks with high values of PC1 are usually to be made from simple syrup, those with low values of PC1 are usually made from powdered sugar. From the two largest bars in PC2, we can see that it highlights the vermouth vs. non-vermouth distinction.
-
It is often easier read the components when the bars are sorted according to their magnitude. The usual ggplot approach to reordering axes labels, using either
reorder()or releveling the associated factor, will reorder all the facets in the same way. If we want to reorder each facet on its own, we can use thereorder_withinfunction coupled withscale_*_reordered, both from thetidytextpackage. -
Next, we can visualize the scores of each sample with respect to these components. The plot below shows (zi1,zi2). Suppose that the columns of Φ are φ1, …, φK. Then, since xi = φ1zi1 + φ2zi2, the samples have large values for variables with large component values in the coordinate directions where zi is farther along.
-
We conclude with some characteristics of PCA, which can guide the choice between alternative dimensionality reduction methods.
- Global structure: Since PCA is looking for high-variance overall, it tends to focus on global structure.
- Linear: PCA can only consider linear combinations of the original features. If we expect nonlinear features to be more meaningful, then another approach should be considered.
- Interpretable features: The PCA components exactly specify how to construct each of the derived features.
- Fast: Compared to most dimensionality reduction methods, PCA is quite fast. Further, it is easy to implement approximate versions of PCA that scale to very large datasets.
- Deterministic: Some embedding algorithms perform an optimization process, which means there might be some variation in the results due to randomness in the optimization. In contrast, PCA is deterministic, with the components being unique up to sign (i.e., you could reflect the components across an axis, but that is the most the results might change).